skku_profiles Module

Principle

If one wishes to analytically generate a height series with the given statistical moments Sk and Ku, a means is to transform a Gaussian series with Johnson’s Translation System. But an alternative means is to use the tangent function:

• in most of industrial cases, the surface heights can be fitted with a tangent function which limits are the parameters
• it’s possible to cover a large (Sk, Ku) domain with these 2 parameters: the starting point $\alpha$ and the ending point $\beta$ of the tangent height series. $\alpha$ close to $-\frac{\pi}{2}$ generates deep pits, and $\beta$ close to $\frac{\pi}{2}$ generates high pics.
• the four first statistical moments can be analytically determined, as functions of $\alpha$ and $\beta$
• the four first statistical moments can be linked to the analytical expressions so that the calculus are very fast
• an optimization process is used to choose the tangent limits when Sk and Ku are given.

The i$^{th}$ surface height $\eta_i$ is expressed as: $$\eta_i = \tan(x_i)=\tan \left[ -\frac{\pi}{2}(1-a) + \dfrac{i-1}{n-1} \frac{\pi}{2} [2-(a+b)] \right]$$

with $x_i \in \left[ -\frac{\pi}{2}(1-a),\frac{\pi}{2} (1-b) \right]$ and $i \in \{1,\ldots,n\}$. As explained above the limits are $\alpha = -\frac{\pi}{2}(1-a)$ and $\beta = \frac{\pi}{2}(1-a)$

Statistical moments

$$\begin{align*} \text{mu} = \mu &=\frac{1}{n} \sum_{i=1}^{n} \eta_i \\ \text{va} = \sigma^2 &=\frac{1}{n} \sum_{i=1}^{n} (\eta_i -\mu)^2 \\ \text{Sk} &=\frac{1}{n} \sum_{i=1}^{n} \left( \dfrac{\eta_i -\mu}{\sigma} \right)^3 \\ \text{Ku} &=\frac{1}{n} \sum_{i=1}^{n} \left( \dfrac{\eta_i -\mu}{\sigma} \right)^4 \\ \end{align*}$$

Transformation of a $\eta$ data set sum into an integral

The use of an analytical representation of the heights is of limited interest if the sums, as expressed above, cannot be avoided because it becomes time consuming for large $n$.

So, how will be the statistical moments calculated in a discrete problem?

… recalling that Simpson’s method involves such sums and that it links it to the function integral.

NB : it is considered that $n$ is an even number, so $n=2p$

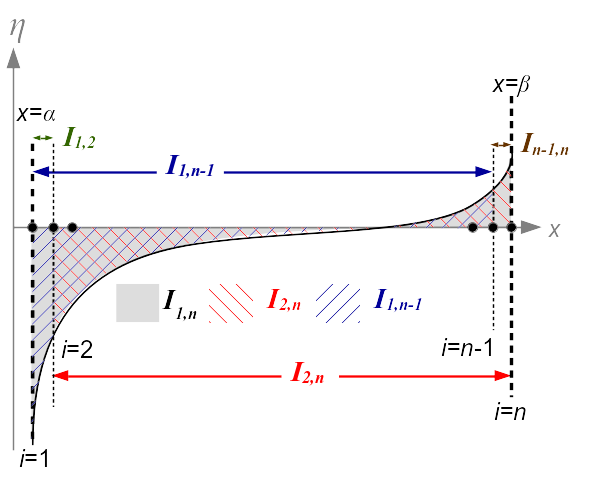
It can be deduced from the figure: $$\begin{align*} I_{1,n-1} = I_{1,2p-1} &= \frac{h}{3} \left( \eta_1 +4\sum_{i=1}^{p-1}\eta_{2i} +2\sum_{i=2}^{p-1}\eta_{2i-1} +\eta_{2p-1} \right) \\ I_{2,n } = I_{2,2p } &= \frac{h}{3} \left( \eta_2 +2\sum_{i=2}^{p-1}\eta_{2i} +4\sum_{i=2}^{p }\eta_{2i-1} +\eta_{2p } \right) \end{align*}$$

As for the borders: $$\begin{align*} I_{ 1, 2} &= \frac{h}{6} \left( \eta_{1 } +4\eta_{ 1+0.5} +\eta_{2 } \right) \\ I_{2p-1,2p} &= \frac{h}{6} \left( \eta_{2p-1} +4\eta_{2p-0.5} +\eta_{2p} \right) \end{align*}$$

As a result: $$\begin{align*} \mathcal{I} &= \int_\alpha^\beta \eta(x)dx \\ &\approx I_{1,n} \\ &= \frac{1}{2} [ I_{1,2} +I_{2,n} +I_{1,n-1}+I_{n-1,n} ] \end{align*}$$

therefore: $$\frac{1}{n} I_{1,n} = \frac{1}{n} \sum_{i=1}^{n}\eta_{i} = \frac{n-1}{n(b-a)}\mathcal{I} +\frac{1}{12n}\left[ 9(\eta_1 +\eta_n) +(\eta_2 +\eta_{n-1}) -4(\eta_{1.5} +\eta_{n-0.5}) \right]$$

Extension

A formula that links the mean of a sum to a function integral has been determined. The same goes for the standard deviation which is the mean of the sum of squares. The same process applies therefore to the four statistical moments, provided that one is able to analytically determine the integrals (Maxima and Mathematica are useful tools).

• mu is calculated as explained above
• when va is calculated, $\eta_i$ is replaced by $\left[ \dfrac{\eta_i -\text{mu}}{\text{si}} \right]^2$ with si=1
• when Sk is calculated, $\eta_i$ is replaced by $\left[ \dfrac{\eta_i -\text{mu}}{\text{si}} \right]^3$
• when Ku is calculated, $\eta_i$ is replaced by $\left[ \dfrac{\eta_i -\text{mu}}{\text{si}} \right]^4$