compute_prc_tables_reynolds_supg Subroutine
private subroutine compute_prc_tables_reynolds_supg(fe_f, e)
Note
Subroutine to calculate the precomputed tables on a FE_FILM REYNOLDS EQUATION DISCRETIZATION
\(
\def\scall{{ \, \tiny{\bullet} \, }}
\)
The Reynolds' equation writes:
\[
\text{div}\left( \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \right) = 6 \, \text{div}\left( \rho h \, \vec{u} \right)
\]
Over each element \( \Omega_e \), the equation is multiplied by the weighting function \( W_i \).
Owing the relationship:
\[
b \, \text{div}\vec{a} = \text{div} (b\,\vec{a}) - \vec{a} \scall \overrightarrow{\text{grad}}b
\]
the equation becomes:
\[
\begin{split}
\int \!\!\! \int_{\Omega_e} \text{div} \left( \frac{\rho h^3}{\mu} W_i \, \overrightarrow{\text{grad}} \, p \right) d\Omega_e &-
\int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \, \scall \, \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e = \\
\int \!\!\! \int_{\Omega_e} 6 \, \text{div} \left( \rho h W_i \, \vec{u} \right) \, \mathrm{d}\Omega_e &-
\int \!\!\! \int_{\Omega_e} 6 \, \rho h \, \vec{u} \, \scall \, \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e
\end{split}
\]
\( W_i \) vanishes on \( \Omega_e \) frontier \( \Gamma_e \), then according Green's formula:
\[
\int \!\!\! \int_{\Omega_e} \text{div} \left( \frac{\rho h^3}{\mu} W_i \, \overrightarrow{\text{grad}} \, p \right) \mathrm{d}\Omega_e =
\oint_{\Gamma_e} \frac{\rho h^3}{\mu} W_i \, \overrightarrow{\text{grad}} \, p \scall \vec{n} \, \mathrm{d}\Gamma_e = 0
\]
In the same manner, if the right handside is handled likewise:
\[
\int \!\!\! \int_{\Omega_e} 6 \, \text{div} \left( \rho h W_i \, \vec{u} \right) \, \mathrm{d}\Omega_e =
\oint_{\Gamma_e} 6 \, \rho h W_i \, \vec{u} \scall \vec{n} \, \mathrm{d}\Gamma_e = 0
\]
and then:
\begin{equation} \label{trans}
\int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \scall \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e =
\int \!\!\! \int_{\Omega_e} 6 \, \rho h \, \vec{u} \scall \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e
\end{equation}
If the right handside isn't transformed:
\begin{equation} \label{notrans}
\int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \scall \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e =
\int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, W_i \, \mathrm{d}\Omega_e
\end{equation}
Equation \eqref{notrans} is more suitable when linear shape functions are use with SUPG, otherwise, using equation \eqref{trans}, \( \overrightarrow{\text{grad}} \, W_i = \overrightarrow{\text{grad}} \, N_i \).
As:
\begin{align*}
\int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, N_i \, \mathrm{d}\Omega_e & = -\int \!\!\! \int_{\Omega_e} 6 \, \rho h \, \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e \\
\vec{\alpha} & = a \, \vec{u}
\end{align*}
then:
\begin{align*}
\int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, W_i \, \mathrm{d}\Omega_e
& = + \int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, \left( N_i + \vec{\alpha} \scall \overrightarrow{\text{grad}} \, N_i \right) \mathrm{d}\Omega_e \\
& = - \int \!\!\! \int_{\Omega_e} 6 \, \rho h \, \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e \\
& \phantom{ = } + \int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, \vec{\alpha} \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e \\
& = -\int \!\!\! \int_{\Omega_e} 6 \, \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \left( \rho h - \vec{\alpha} \scall \overrightarrow{\text{grad}} \, \rho h \right) \mathrm{d}\Omega_e
\end{align*}
Approximating \( \rho h \) with the shape functions, \( \rho h = [\rho h]_k \, N_k \), leads to:
\begin{align*}
\int \!\!\! \int_{\Omega_e} 6 \, \text{div}\left( \rho h \, \vec{u} \right) \, W_i \, \mathrm{d}\Omega_e & = -\int \!\!\! \int_{\Omega_e} 6 \, \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \, [\rho h]_k \, \left( N_k - \vec{\alpha} \scall \overrightarrow{\text{grad}} \, N_k \right) \mathrm{d}\Omega_e
\end{align*}
Let \( \tilde{N_k} \) be the upwind shape function, so that \( \tilde{N_k} = N_k - \vec{\alpha} \scall \overrightarrow{\text{grad}} \, N_k \) thus:
\begin{equation} \label{reynolds}
\int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \scall \overrightarrow{\text{grad}} \, W_i \, \mathrm{d}\Omega_e =
-\int \!\!\! \int_{\Omega_e} 6 \, \widetilde{\rho h} \; \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e
\end{equation}
provided that \( \widetilde{\rho h} = [\rho h]_k \, \tilde{N}_k \).
Let \( R_i \) be the residual of equation \eqref{reynolds} defined as:
\begin{equation*}
R_i = \int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, p \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e
- \int \!\!\! \int_{\Omega_e} 6 \, \widetilde{\rho h} \; \vec{u} \scall \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e
\end{equation*}
Hence, defining \( \frac{\partial \rho}{\partial p_j} \) as \( \left[ \frac{\partial \rho}{\partial p} \right]_j N_j \) :
\begin{align}
\frac{\partial R_i}{\partial p_j} = R_{ij} =
+ & \int \!\!\! \int_{\Omega_e} \frac{\rho h^3}{\mu} \overrightarrow{\text{grad}} \, N_j \, \scall \, \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e \nonumber \\
+ & \int \!\!\! \int_{\Omega_e} \frac{ h^3}{\mu} \left[ \frac{\partial \rho}{\partial p} \right]_j \! N_j \, \overrightarrow{\text{grad}} \, p \, \scall \, \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e \nonumber \\
- & \int \!\!\! \int_{\Omega_e} 6 \, \left[ h \frac{\partial \rho}{\partial p} \right]_j \tilde{N_j} \; \vec{u} \, \scall \, \overrightarrow{\text{grad}} \, N_i \, \mathrm{d}\Omega_e
\end{align}
and \( b_i = -R_i \).
UPWINDING COEFFICIENTS
Zienkiewicz, "The Finite Element Method for Fluid Dynamics", 7th, p30, p50
The simplest form of Convection-Diffusion-Reaction Equation is one in which the unknown is a scalar.
It is a set of conservation laws arising from a balance of the quantity with fluxes entering and leaving a control volume:
$$
\frac{\partial \phi}{\partial t} +\frac{\partial (U_i \phi)}{\partial x_i} -
\frac{\partial}{\partial x_i} \left( k\frac{\partial \phi}{\partial x_i} \right) +Q =0
$$
\(U_i\) is a known velocity field and \(\phi\) is a scalar quantity being transported by this velocity.
Diffusion can also exist and \(k\) is the diffusion coefficient. The term \(Q\) represents any external
sources of the quantity \(\phi\).
Using the fact that \(h/L\ll 1\), that the fluid is Newtonian, and that the viscosity and density are constant
through the film direction, the following Reynolds equation is obtained:
$$
\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\mu}\frac{\partial p}{\partial x} \right) +
\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\mu}\frac{\partial p}{\partial y} \right)= \\
\frac{1}{2}\frac{\partial }{\partial x}\left[ \left(U_1+U_2\right)\rho h \right]+
\frac{1}{2}\frac{\partial }{\partial y}\left[ \left(V_1+V_2\right)\rho h \right]+
\frac{\partial }{\partial t}\left(\rho h \right)
$$
Identifying the different terms leads to:
$$
k=\frac{\rho h^3}{\mu} \text{ ; } \phi = p \text{ ; } U_i = 6 v_i h\frac{\partial \rho}{\partial p} \text{ with } \boldsymbol{v}=
\begin{pmatrix}
U_2 \\
V_2
\end{pmatrix}
$$

In the bidimensional case, the Peclet parameter is a vector:
$$
\boldsymbol{Pe} = \frac{1}{k} \left( \boldsymbol{U}\frac{Le}{2} \right)=
\begin{pmatrix}
Pe_x \\
Pe_y
\end{pmatrix}
$$
where \(Le\) is the element length.
The Peclet numbers of the Reynolds equation are therefore defined as:
$$
Pe_x = \frac{6\mu(Le/2) U_2}{\rho h^2} \frac{\partial \rho}{\partial p} \\
Pe_y = \frac{6\mu(Le/2) V_2}{\rho h^2} \frac{\partial \rho}{\partial p}
$$
The optimal upwinding coefficient is:
$$
\alpha = \coth{Pe} -\frac{1}{Pe}
$$
with \(Pe=||\boldsymbol{Pe}||\)
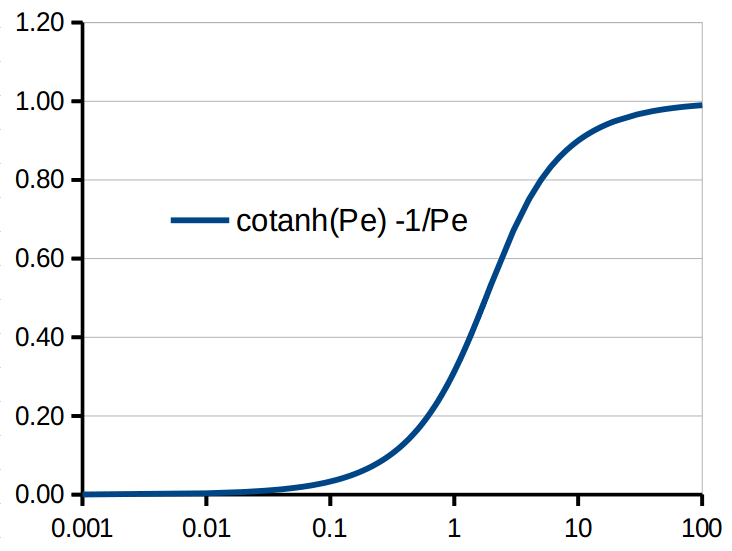
Using Zienkiewicz scheme:


PRECOMPUTED INTEGRATION PARTS
\[
x(\xi,\eta) = \sum\limits_{nodes \; i} x_i \times N_{i}(\xi,\eta) \\
y(\xi,\eta) = \sum\limits_{nodes \; i} y_i \times N_{i}(\xi,\eta)
\]
Let \(c_i\) be defined by:
\[
c_1 = \frac{\partial x}{\partial \xi } \; ; \;
c_2 = \frac{\partial y}{\partial \xi } \; ; \;
c_3 = \frac{\partial x}{\partial \eta} \; ; \;
c_4 = \frac{\partial y}{\partial \eta} \\
c_5 = det \begin{pmatrix}
c_1 & c_2 \\
c_3 & c_4
\end{pmatrix} = c_1 c_4 - c_2 c_3
\]
It must be remembered that the functions are first order, *ie* the \(x\) derivative with respect to \(\xi\) only depends on \(\eta\).
\[
h(x,y)^3 = \sum\limits_{nodes \; k} h^3_{k} \times N_{k}(x,y)
\]
The same goes for \(\rho\) and \(\mu\). Therefore, at Gauss point \((i,j)\), \(\rho h^3 /\mu\) can be precalculated:
\[
\begin{align*}
vcal(2, i, j) &= \left( \sum\limits_{nodes \; k} h^3_{k} \times N_{k}(x_i, y_j) \right).
\left( \sum\limits_{nodes \; k} \rho_{k} \times N_{k}(x_i, y_j) \right).
\left( \sum\limits_{nodes \; k} \frac{1}{\mu_{k}} \times N_{k}(x_i, y_j) \right)\\
&= (h^3)_{ij} \; (\rho)_{ij} \; \left(\frac{1}{\mu}\right)_{ij}
\end{align*}
\]
Likewise:
\[
\begin{align*}
vcal( 3, i, j) &= 6\, (V\!x)_{ij} \\
vcal( 4, i, j) &= 6\, (V\!y)_{ij} \\
vcal( 5, i, j) &= -\rho_k h_k \,.\, \tilde{N}_{k}(x_i, y_j) \\
vcal( 6, i, j) &= K_{ij}\left[ (\rho)_{ij} (h^3)_{ij} \left(\frac{1}{\mu}\right)_{ij} \left(\frac{\partial p}{\partial x}\right)_{ij} \right] \\
vcal( 7, i, j) &= K_{ij}\left[ (\rho)_{ij} (h^3)_{ij} \left(\frac{1}{\mu}\right)_{ij} \left(\frac{\partial p}{\partial y}\right)_{ij} \right] \\
vcal( 8, i, j) &= K_{ij}\left[ 6 \; (V\!x)_{ij} \left(\rho_k h_k \tilde{N}_k (x_i, y_j)\right) \right] \\
vcal( 9, i, j) &= K_{ij}\left[ 6 \; (V\!y)_{ij} \left(\rho_k h_k \tilde{N}_k (x_i, y_j)\right) \right] \\
vcal(10, i, j) &= K_{ij}\left[ (h^3)_{ij} \left(\frac{1}{\mu}\right)_{ij} \left(\frac{\partial p}{\partial x}\right)_{ij} \right] \\
vcal(11, i, j) &= K_{ij}\left[ (h^3)_{ij} \left(\frac{1}{\mu}\right)_{ij} \left(\frac{\partial p}{\partial y}\right)_{ij} \right] \\
vcal(12, i, j) &= K_{ij}\left[ (p)_{ij} \right]\\
vcal(13, i, j) &= K_{ij}\left[ -\frac{1}{2} (h)_{ij} \left(\frac{\partial p}{\partial x}\right)_{ij} -(\mu)_{ij} (V\!x)_{ij} \left( \frac{1}{h} \right)_{ij} \right]
\end{align*}
\]
with:
\[
vcal(1, i, j) = K_{ij} = c_5 w_i w_j \text{ ; } w_i \text{ Gauss ith weighting coefficient}
\]
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| type(FE_FILM), | intent(inout) | :: | fe_f | FE film |
||
| integer(kind=I4), | intent(in) | :: | e | element number |
Calls
Called by
Source Code
subroutine compute_prc_tables_reynolds_supg(fe_f, e)
implicit none
type(FE_film), intent(inout) :: fe_f !! *FE film*
integer(kind=I4), intent(in ) :: e !! *element number*
integer(kind=I4) :: i, j, k, ng, nne
logical(kind=I4) :: gaz
real(kind=R8), dimension(MAX_NNE) :: tvx, tvy, th, tp, trho, tmu, tdrdp, tx, ty, tnix, tniy
real(kind=R8), dimension(MAX_NNG) :: wg, pg
real(kind=R8) :: c5, vc1
real(kind=R8) :: Pe_ux, Pe_uy, Pe_u, Pe_vx, Pe_vy, Pe_v, coeff_x, coeff_y, kk
real(kind=R8) :: sx, sy, alpha_u, alpha_ux, alpha_uy, alpha_vx, alpha_vy, alpha_v
real(kind=R8) :: dNidx_p, dNidy_p, Nid_rho_h, Ni_p, Ni_h, Ni_h3, Ni_vx, Ni_vy, Ni_mu, Ni_rho, Ni_inv_h, Ni_inv_mu
real(kind=R8) :: lu, wu, lv, wv
real(kind=R8) :: Ni_drhodp, gradh, gradhx, gradhy, gradp, gradpx, gradpy
real(kind=R8) :: drdp, h, mu, rho, u, ux, uy, v, vx, vy
real(kind=R8), dimension(MAX_NNE) :: vni4, vni4x, vni4y, vni4d
real(kind=R8), dimension(14) :: vcal
!============================================
!> {!MUSST/src/inc_doc/Reynolds_discretization.md!}
!============================================
!============================================
!> {!MUSST/src/inc_doc/upwinding_coefficients.md!}
!============================================
gaz = (fe_f%data_f%fl%fluid_type==GP)
nne = fe_f%m%el_t(e)
! values on the nodes
do i = 1, nne
j = fe_f%m%con(e, i)
tx(i) = fe_f%m%x(j) ! coordinates
ty(i) = fe_f%m%y(j)
tvx(i) = fe_f%vn (j, VX_N) ! velocities
tvy(i) = fe_f%vn (j, VY_N)
th(i) = fe_f%vn (j, H_N) ! heigth
tp(i) = fe_f%vn (j, P_N) ! pressure
trho(i) = fe_f%vn (j, RHO_N) ! density
tmu(i) = fe_f%vn (j, MU_N) ! viscosity
tdrdp(i) = fe_f%vn (j, DRHODP_N) ! viscosity derivative regarding P
enddo
c5 = dj4(ksi=0._R8, eta=0._R8, x=tx(1:nne), y=ty(1:nne))
call calc_ni4_xy_derivatives(ni4x = tnix(1:nne), &
ni4y = tniy(1:nne), &
ksi = 0._R8, &
eta = 0._R8, &
x = tx(1:nne), &
y = ty(1:nne), &
dj = c5)
! addition of the groove depth
th(1:nne) = th(1:nne) + fe_f%vc(e, HG_C)
ux = sum(tvx(1:nne))/nne
uy = sum(tvy(1:nne))/nne
u = sqrt( ux**2 + uy**2 )
h = sum(th (1:nne))/nne
drdp = sum(tdrdp(1:nne))/nne
mu = sum(tmu (1:nne))/nne
rho = sum(trho (1:nne))/nne
gradpx = sum( tp(1:nne)*tnix(1:nne) )
gradpy = sum( tp(1:nne)*tniy(1:nne) )
gradp = sqrt( gradpx**2 +gradpy**2 )
gradhx = sum( th(1:nne)*tnix(1:nne) )
gradhy = sum( th(1:nne)*tniy(1:nne) )
gradh = sqrt( gradhx**2 +gradhy**2 )
kk = 6*(drdp/rho)*mu*(1./h**2)
! Gauss points
ng = fe_f%prc%ng
pg(1:ng) = fe_f%prc%pg(1:ng)
wg(1:ng) = fe_f%prc%wg(1:ng)
if (gaz) then
v = -(h**2)/(6*mu)
vx = v*gradpx
vy = v*gradpy
v = sqrt( vx**2 + vy**2 )
call length_width_elem(spdx = ux, & ! in, speed u along x
spdy = uy, & ! in, speed u along y
x = tx, & ! in, element x coordinates
y = ty, & ! in, element y coordinates
length = lu, & ! out, length along u
width = wu) ! out, width
call length_width_elem(spdx = vx, & ! in, speed v along x
spdy = vy, & ! in, speed v along y
x = tx, & ! in, element x coordinates
y = ty, & ! in, element y coordinates
length = lv, & ! out, length along v
width = wv) ! out, width
! Peclet number related to u
Pe_ux = ux * (lu/2) * kk
Pe_uy = uy * (lu/2) * kk
Pe_u = sqrt(Pe_ux**2 +Pe_uy**2)
! Peclet number related to v
Pe_vx = vx * (wu/2) * kk
Pe_vy = vy * (wu/2) * kk
Pe_v = sqrt(Pe_vx**2 +Pe_vy**2)
alpha_ux = Pe_ux
alpha_uy = Pe_uy
alpha_u = Pe_u
alpha_v = (h/1.e6)*(u/1.e2)*(mu/1.e-5) * (wu/lu) * ( Pe_vx * (-uy) + Pe_vy * (+ux) )/u
alpha_vx = alpha_v * (-uy)/u
alpha_vy = alpha_v * (+ux)/u
alpha_v = sqrt(alpha_vx**2 +alpha_vy**2)
coeff_x = alpha_ux +alpha_vx ; sx = sign(1._R8, coeff_x) ; coeff_x = abs(coeff_x)
coeff_y = alpha_uy +alpha_vy ; sy = sign(1._R8, coeff_y) ; coeff_y = abs(coeff_y)
fe_f%vc(e, PEK_C) = sx*coeff_x
fe_f%vc(e, PEE_C) = sy*coeff_y
else
lu = maxval(tx(1:nne)) -minval(tx(1:nne))
wu = maxval(ty(1:nne)) -minval(ty(1:nne))
lv = lu * ux + wu * uy
Pe_ux = kk * (lv/2)
Pe_uy = 0._R8
if (abs(Pe_ux) < 1.e-2_R8) then
Pe_ux = Pe_ux / 3
else
Pe_ux = 1._R8 / (tanh(Pe_ux)) - 1._R8 / Pe_ux
endif
alpha_vx = 1._r8
alpha_vy = 1._r8
if (u > 0._r8) then
alpha_vx = lv * ux / (2 * (u ** 2))
alpha_vy = lv * uy / (2 * (u ** 2))
endif
fe_f%vc(e, Pek_c) = alpha_vx
fe_f%vc(e, Pee_c) = alpha_vy
endif
!=============================================
!> {!MUSST/src/inc_doc/precomputed_integrations.md!}
!=============================================
do i = 1, ng
do j = 1, ng
vni4(1:nne) = fe_f%prc%vni4(1:nne, i, j)
! computation of the shape function derivatives
c5 = dj4(ksi=pg(i), eta=pg(j), x=tx(1:nne), y=ty(1:nne))
call calc_ni4_xy_derivatives(ni4x = vni4x(1:nne), &
ni4y = vni4y(1:nne), &
ksi = pg(i), &
eta = pg(j), &
x = tx(1:nne), &
y = ty(1:nne), &
dj = c5)
if (c5 < 0) stop 'compute_prc_tables_reynolds_supg: jacobian negative for elt'
if (gaz) then
do k = 1, nne
vni4d(k) = ni4_up_2d(k, pg(i), pg(j), (/coeff_x, coeff_y/), (/sx, sy/))
enddo
else
vni4d(1:nne) = vni4(1:nne) -alpha_vx*Pe_ux*vni4x(1:nne) -alpha_vy*Pe_ux*vni4y(1:nne)
endif
fe_f%prc%vni4x(1:nne, i, j) = vni4x(1:nne)
fe_f%prc%vni4y(1:nne, i, j) = vni4y(1:nne)
fe_f%prc%vni4d(1:nne, i, j) = vni4d(1:nne)
! computation of the coefficients for the Reynolds equation
vc1 = wg(i) * wg (j) * c5
dNidx_p = sum(vni4x(1:nne) * tp(1:nne))
dNidy_p = sum(vni4y(1:nne) * tp(1:nne))
Nid_rho_h = sum(vni4d(1:nne) * trho(1:nne) * th(1:nne))
Ni_p = sum( vni4(1:nne) * tp(1:nne))
Ni_h = sum( vni4(1:nne) * th(1:nne))
Ni_h3 = sum( vni4(1:nne) * th(1:nne)**3)
Ni_vx = sum( vni4(1:nne) * tvx(1:nne))
Ni_vy = sum( vni4(1:nne) * tvy(1:nne))
Ni_mu = sum( vni4(1:nne) * tmu(1:nne))
Ni_rho = sum( vni4(1:nne) * trho(1:nne))
Ni_inv_h = sum( vni4(1:nne) * (1._R8 / th(1:nne)))
Ni_inv_mu = sum( vni4(1:nne) * (1._R8 / tmu(1:nne)))
Ni_drhodp = sum( vni4(1:nne) * tdrdp(1:nne))
vcal( 1) = vc1
vcal( 2) = vc1 * Ni_h3 * Ni_rho * Ni_inv_mu
vcal( 3) = vc1 * 6*Ni_vx * Ni_h
vcal( 4) = vc1 * 6*Ni_vy * Ni_h
vcal( 5) = 0
vcal( 6) = vc1 * Ni_h3 * Ni_inv_mu * Ni_rho * dNidx_p
vcal( 7) = vc1 * Ni_h3 * Ni_inv_mu * Ni_rho * dNidy_p
vcal( 8) = vc1 * 6*Ni_vx * Nid_rho_h
vcal( 9) = vc1 * 6*Ni_vy * Nid_rho_h
vcal(10) = vc1 * Ni_h3 * Ni_inv_mu * dNidx_p
vcal(11) = vc1 * Ni_h3 * Ni_inv_mu * dNidy_p
vcal(12) = vc1 * Ni_p
vcal(13) = vc1 * (-dNidx_p * Ni_h/2 - Ni_mu * Ni_vx * Ni_inv_h)
vcal(14) = vc1 * (-dNidy_p * Ni_h/2 - Ni_mu * Ni_vy * Ni_inv_h)
fe_f%prc%vcal(1:14, i ,j) = vcal(1:14)
enddo
enddo
!=============================================
!> {!MUSST/css/button.html!}
!=============================================
return
endsubroutine compute_prc_tables_reynolds_supg