asfc Module
- Arthur Francisco
- may, 03 2019
- 1.0.0
- 1274 statements
- Source File
A fast and accurate way of determining the area-scale fractal analysis complexity parameter Asfc
Principle
The ISO 25178-2:2012(E) states that
“The observed area is calculated as a function of scale by a series of virtual tiling exercises covering the measured surface in a patchwork fashion. The areas of the tiles, or patches, represent the areal scales of observation. The tiling exercises are repeated with tiles of progressively smaller areas to determine the observed areas to determine the observed areas as a function of the areal scales of observation.
Then, the function log(relative area)=f(log(element area)) can be determined. The area-scale fractal analysis complexity parameter Asfc is defined as a thousand times minus the line slope:.
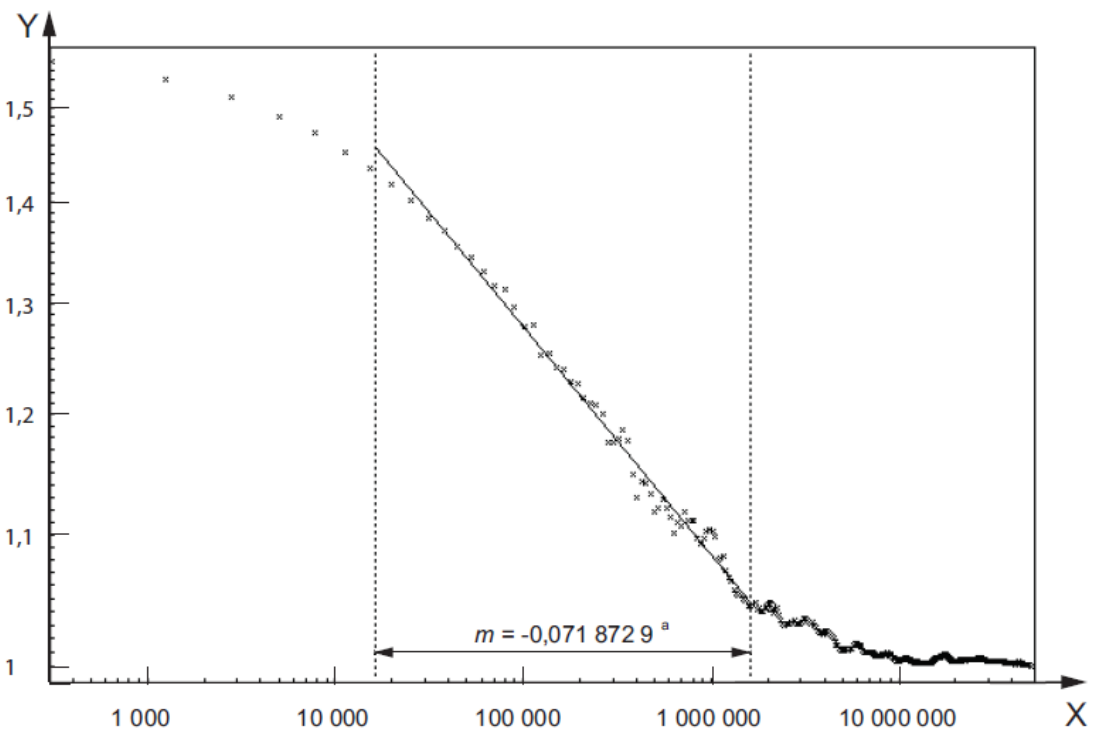
Determining the steepest part of the curve in a robust way
It can be reasonably stated that most of relative area plots are S-shaped, even if the trail can be more linear than curved. Instead of arbitrarily defining a “central” region where to calculate the maximum of the slope, the whole curve is fitted with a family Tn, of monotonic functions.
In most cases leads to an accurate fit, especially in the linear part of the curve, where the studied surface exhibits self-similarity properties.
The proposed model is parsimonious — only four parameters have to be determined, with a least square procedure for instance — and then doesn’t suffer from overfitting. Some surfaces have better fit results with but it doesn’t change much the Asfc value. The location of the steepest part is analytically determined by canceling the second derivative of Tn. A simple calculus yields:
when , it reduces to .
To address the computation efficiency question — induced by the series of tiling exercises — the surface itself isn’t tiled as explained in ISO 25178. The different scales are those of the grids that are used to discretize the surface.
The grids are chosen regular with lateral steps from (hx, hy) for the finest grid to (Hx, Hy) for the largest grid. The finest grid is the one of the original surface, and the coarsest grid is an 8 × 8 grid.
The original grid is the only one for which the surface points match the grid points, for the other grids the surface heights are obtained by interpolation.
The intermediate grids are defined so that the element size has a geometric progression, hence its location is evenly spaced on a logarithm axis.
Three surface interpolation methods are tested: linear (linear Finite Elements), interpolant cubic splines, and Hermite (Hermite Finite Elements)
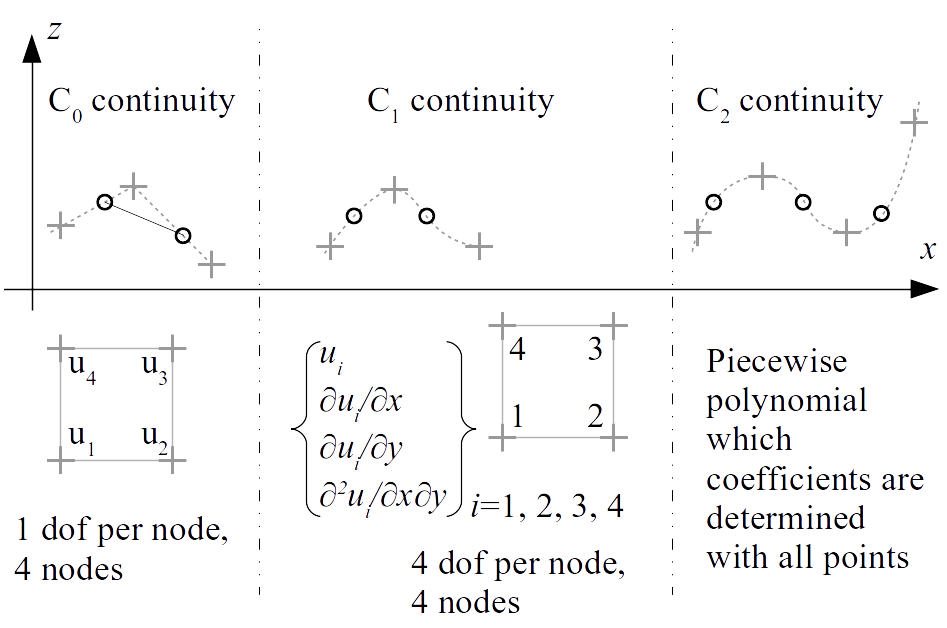
The chosen interpolation methods are: left, linear FE - middle, Hermite FE - right, cubic spline. “dof” stands for “degree of freedom”. In the upper part, one can see that from left to right, the smoothness increases. Below, calling u the unknown, it can be seen that increasing smoothness requires to take into account more derivatives. As the spline method guarantees curvature continuity, the unknown and its derivatives must be computed globally.
The surface heights are computed on the different grids with one of the three interpolation procedures that are proposed – linear (finite element style), Hermite (finite element style) and cubic spline. 128 grids are used to draw the relative area curve. Provided the interpolating function f(x,y), the area of a surface element defined on is obtained by integration of
Such an expression being barely easy to analytically integrate, the Gauss integrating method is used with two points in each direction, which ensures the exact integration of a third degree polynomial on both directions.
Used by
Variables
| Type | Visibility | Attributes | Name | Initial | |||
|---|---|---|---|---|---|---|---|
| integer(kind=I4), | private, | parameter | :: | hermite | = | 4 |
Hermite interpolation between grids |
| integer(kind=I4), | private, | parameter | :: | kx | = | 3 |
x bspline order |
| integer(kind=I4), | private, | parameter | :: | ky | = | 3 |
y bspline order |
| integer(kind=I4), | private, | parameter | :: | larg0 | = | 8 |
roughest grid |
| integer(kind=I4), | private, | parameter | :: | lin_all | = | 0 |
linear interpolation between grids |
| logical(kind=I4), | private, | parameter | :: | live | = | .false. |
default for file outputs |
| integer(kind=I4), | private, | parameter | :: | long0 | = | 8 |
roughest grid |
| integer(kind=I4), | private, | parameter | :: | method_asfc | = | hermite |
default |
| integer(kind=I4), | private, | parameter | :: | nb_beta | = | 4 |
number of parameters to be determined when optimizing |
| integer(kind=I4), | private, | parameter | :: | npp | = | 128 |
number of points for the asfc determination |
| logical(kind=I4), | private, | parameter | :: | out_her | = | live |
default for file outputs, Hermite case |
| logical(kind=I4), | private, | parameter | :: | out_lin | = | live |
default for file outputs, linear case |
| logical(kind=I4), | private, | parameter | :: | out_spl | = | live |
default for file outputs, spline case |
| logical(kind=I4), | private, | parameter | :: | out_ter | = | live |
default for terminal output |
| integer(kind=I4), | private, | parameter | :: | spl_all | = | 2 |
spline interpolation between grids |
| integer(kind=I4), | private | :: | unit_out_her |
output unit for the Hermite case |
|||
| integer(kind=I4), | private | :: | unit_out_lin |
output unit for the linear case |
|||
| integer(kind=I4), | private | :: | unit_out_spl |
output unit for the spline case |
Functions
private function df_boltz(xi, beta, n_beta, ivar)
Fitting function partial derivatives.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi |
data point |
||
| real(kind=R8), | intent(inout), | dimension(1:n_beta) | :: | beta |
parameter vector |
|
| integer(kind=I4), | intent(in) | :: | n_beta |
number of parameters |
||
| integer(kind=I4), | intent(in) | :: | ivar |
parameter number |
Return Value real(kind=r8)
private function dn_i(xi, i)
1D shape function derivative, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| integer(kind=I4), | intent(in) | :: | i |
Return Value real(kind=r8)
private function dnq_et_i(xi, et, i, j)
2D shape function derivative, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| real(kind=R8), | intent(in) | :: | et | |||
| integer(kind=I4), | intent(in) | :: | i | |||
| integer(kind=I4), | intent(in) | :: | j |
Return Value real(kind=r8)
private function dnq_xi_et_i(xi, et, i, j)
2D shape function , derivative, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| real(kind=R8), | intent(in) | :: | et | |||
| integer(kind=I4), | intent(in) | :: | i | |||
| integer(kind=I4), | intent(in) | :: | j |
Return Value real(kind=r8)
private function dnq_xi_i(xi, et, i, j)
2D shape function derivative, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| real(kind=R8), | intent(in) | :: | et | |||
| integer(kind=I4), | intent(in) | :: | i | |||
| integer(kind=I4), | intent(in) | :: | j |
Return Value real(kind=r8)
private function f_boltz(xi, beta, n_beta)
Fitting function.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi |
data point |
||
| real(kind=R8), | intent(inout), | dimension(1:n_beta) | :: | beta |
parameter vector |
|
| integer(kind=I4), | intent(in) | :: | n_beta |
number of parameters |
Return Value real(kind=r8)
private function locate(n, xx, x)
Function that returns the location of an element in a vector.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| integer(kind=I4), | intent(in) | :: | n |
vector length |
||
| real(kind=R8), | intent(in), | dimension(1:n) | :: | xx |
vector |
|
| real(kind=R8), | intent(in) | :: | x |
value to locate |
Return Value integer(kind=i4)
private function locate2(n, xx, x, eps)
Function that returns the location of an element in a vector.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| integer(kind=I4), | intent(in) | :: | n |
vector length |
||
| real(kind=R8), | intent(in), | dimension(1:n) | :: | xx |
vector |
|
| real(kind=R8), | intent(in) | :: | x |
value to locate |
||
| real(kind=R8), | intent(in) | :: | eps |
small value for comparisons of reals |
Return Value integer(kind=i4)
private function n_i(xi, i)
1D shape function, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| integer(kind=I4), | intent(in) | :: | i |
Return Value real(kind=r8)
private function nq_i(xi, et, i, j)
2D shape function, quadratic case.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in) | :: | xi | |||
| real(kind=R8), | intent(in) | :: | et | |||
| integer(kind=I4), | intent(in) | :: | i | |||
| integer(kind=I4), | intent(in) | :: | j |
Return Value real(kind=r8)
Subroutines
private subroutine calcul_aire(tab_in, long, larg, hx, hy, aire)
Return the area of a surface
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:long,1:larg) | :: | tab_in |
surface array |
|
| integer(kind=I4), | intent(in) | :: | long |
2D array length |
||
| integer(kind=I4), | intent(in) | :: | larg |
2D array width |
||
| real(kind=R8), | intent(in) | :: | hx |
increment along x |
||
| real(kind=R8), | intent(in) | :: | hy |
increment along y |
||
| real(kind=R8), | intent(out) | :: | aire |
computed area |
private subroutine calcul_asfc(tab_in, scal, asfc_res, omp)
Return the asfc of a surface regarding the default parameter method_asfc
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:scal%xres, 1:scal%yres) | :: | tab_in |
input surface |
|
| type(SCALE_SURF), | intent(in) | :: | scal |
surface characteristics |
||
| real(kind=R8), | intent(out), | dimension(1:2) | :: | asfc_res |
result: asfc, adjustment factor |
|
| logical(kind=I4), | intent(in) | :: | omp |
with openmp ? |
public subroutine calcul_asfc_hermite(tab_in, scal, asfc_res, omp)
Return the asfc of a surface. The different grids are obtained by Hermite interpolation
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:scal%xres, 1:scal%yres) | :: | tab_in |
input surface |
|
| type(SCALE_SURF), | intent(in) | :: | scal |
surface characteristics |
||
| real(kind=R8), | intent(out), | dimension(1:2) | :: | asfc_res |
result: asfc, adjustment factor |
|
| logical(kind=I4), | intent(in) | :: | omp |
with openmp ? |
private subroutine calcul_asfc_lin_all(tab_in, scal, asfc_res)
Return the asfc of a surface. The different grids are obtained by linear interpolation
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:scal%xres, 1:scal%yres) | :: | tab_in |
input surface |
|
| type(SCALE_SURF), | intent(in) | :: | scal |
surface characteristics |
||
| real(kind=R8), | intent(out), | dimension(1:2) | :: | asfc_res |
result: asfc, adjustment factor |
private subroutine calcul_asfc_spl_all(tab_in, scal, asfc_res)
Return the asfc of a surface. The different grids are obtained by spline of degree 3
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:scal%xres, 1:scal%yres) | :: | tab_in |
input surface |
|
| type(SCALE_SURF), | intent(in) | :: | scal |
surface characteristics |
||
| real(kind=R8), | intent(out), | dimension(1:2) | :: | asfc_res |
result: asfc, adjustment factor |
public subroutine indice_fractal(tab_in, long, larg, indf)
Function that returns the fractal dimension with the box counting method
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(in), | dimension(1:long, 1:larg) | :: | tab_in |
surface array |
|
| integer(kind=I4), | intent(in) | :: | long |
surface array length |
||
| integer(kind=I4), | intent(in) | :: | larg |
surface array width |
||
| real(kind=R8), | intent(out), | dimension(3) | :: | indf |
result: ordinate at origin, slope, R2 |
private subroutine init_beta_boltz(bt, n_bt, v_x, v_y, n_pt)
Function that initializes the fitting tanh function f_boltz parameters.
Arguments
| Type | Intent | Optional | Attributes | Name | ||
|---|---|---|---|---|---|---|
| real(kind=R8), | intent(out), | dimension(1:n_bt) | :: | bt |
vector of parameters |
|
| integer(kind=I4), | intent(in) | :: | n_bt |
number of parameters |
||
| real(kind=R8), | intent(in), | dimension(1:n_pt) | :: | v_x |
x data to fit |
|
| real(kind=R8), | intent(in), | dimension(1:n_pt) | :: | v_y |
y data to fit |
|
| integer(kind=I4), | intent(in) | :: | n_pt |
data vector length |