filter Module

The morphological filter is a technique in surface processing used to process geometrical structures within a surface.

Imagine a ball rolling over the surface. Depending on the size and shape of the ball, it modifies the surface differently: larger balls can bridge small gaps, while smaller balls can fall into minor crevices.

This filter is particularly useful in operations such as closing and opening, which can help in joining narrow breaks and eliminating small holes within objects in an image, respectively.

The median filter is a non-linear digital filtering technique, often used to remove noise from surfaces.

It works by moving through each point of the surface, and considering a small neighborhood around that element. The filter then replaces the element with the median of its neighboring values. This method is particularly effective because, unlike mean filtering, it can remove noise while preserving edges in the surfaces.

The median filter maintains sharp edges in surfaces and is robust against the introduction of noise.

This median filter is a bit more complex than the classical median filter.

An outlying observation, or “outlier”, is one that appears to deviate markedly from other members of the sample in which it occurs. Therefore no universal procedure exists to remove extra points: it depends on the kind of outliers and the surrounding data.

In the present case several procedures have been tested and the one that best suits our need is the following:

• A 5x5 kernel median filter is applied to S1, giving S2.
• S3 = S1 -S2 represents the S1 deviation from the median.
• S3 is divided in 10 parts in each direction, and for each part the standard deviation is calculated. The global S3 deviation σ is defined as the median value of the 10x10 standard deviations
• Inspired by the normal law, the procedure ends with the substitution of heights, for which abs(S1-S2) > 3σ, by median heights. The cleaned surface which is obtained will be called SA in what follows.

Eventhough the procedure is unusual, it provides satisfactory results in cleaning the primary extracted surfaces, without altering “real” points.

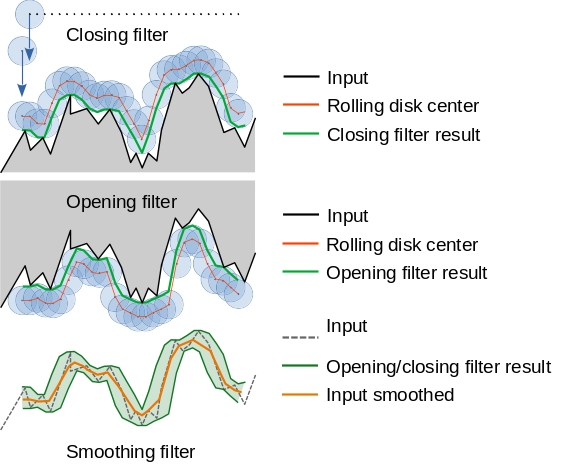
The 2D smoothing kernel with a stencil of [1 2 1] represents a simple, yet effective method for smoothing a surface. This stencil typically forms a part of a larger convolution kernel applied over an image to average height values, effectively reducing noise and detail.

This kernel is often used in conjunction with a similar vertical stencil to create a two-dimensional convolution mask. In practice, the [1 2 1] stencil is one row of a matrix, with possibly a corresponding column vector [1; 2; 1], used to perform a 2D convolution operation on a surface.

When applied, each height in the resulting surface is a weighted average of its neighbors with the weights given by the kernel:

• The central height in the neighborhood receives the highest weight, typically reflecting higher importance or influence on the resulting height value.
• The adjacent heights horizontally (and vertically, when combined with the vertical vector) receive a lower weight than the central height but contribute significantly to the smoothing effect.
• Corner heights, if included by expanding the kernel to a full 2x2 or 3x3 matrix using both horizontal and vertical components, would receive the lowest weights.

In terms of application, the resulting convolution matrix for the two-dimensional case is : $$ \begin{matrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{matrix} $$ This configuration spreads the influence of a single height to its eight neighbors in a weighted manner, with a stronger influence horizontally and vertically, rather than diagonally.

The strength of smoothing is adjusted by normalizing this kernel (dividing all entries by the sum of the entries, which is 16 in the standard case), thereby ensuring that the total influence in the area remains constant, preserving overall height.

EN ISO 16610-61 septembre 2015 - Geometrical product specification (GPS) - Filtration - Part 61: Linear areal filters: Gaussian filters The weighting function of an areal filter has the formula of a rotationally symmetric Gaussian function with a cut-off wavelength, \(\lambda_c\) , given by : $$ S(x,y)=\frac{1}{\alpha^2 \lambda_c^2} \; \exp \left[-\frac{\pi}{\alpha^2} \; \left( \frac{x^2 + y^2}{\lambda_c^2} \right) \right] $$

• \(x\) is the distance from the centre (maximum) of the weighting function in \(X\) direction;
• \(y\) is the distance from the centre (maximum) of the weighting function in \(Y\) direction;
• \(\lambda_c\) is the cut-off wavelength;
• \(\alpha\) is the constant, to provide 50% transmission characteristic at the cut-off \(\lambda_c\). Therefore, \(\displaystyle \alpha = \sqrt{\frac{\log 2}{\pi}}\)

The Gaussian filter is employed in surface processing for reducing detail and noise, effectively smoothing the surface.

This filter utilizes a Gaussian function for calculating the transformation to apply to each point in the surface. It assigns weights to pixels with distances based on the Gaussian function's characteristics, heavily weighting pixels nearer to the central pixel and progressively less to those farther away.

This creates a blurring effect that is very effective at high-frequency noise reduction, leading to a smoother appearance in surfaces.